News
Introduction
Welcome to the Fukuoka MQ challenge project.
Multivariate Quadratic polynomial (MQ) problem is the basis of security for potentially post-quantum crypto systems. The hardness of solving MQ problem depends on a number of parameters, most importantly the number of variables, as well as the number of equations, the size of the base field etc.
MQ Challenge:
For quadratic polynomials fi (i=1,2,...,m) of n variables over a finite field F, consider the following polynomial system:
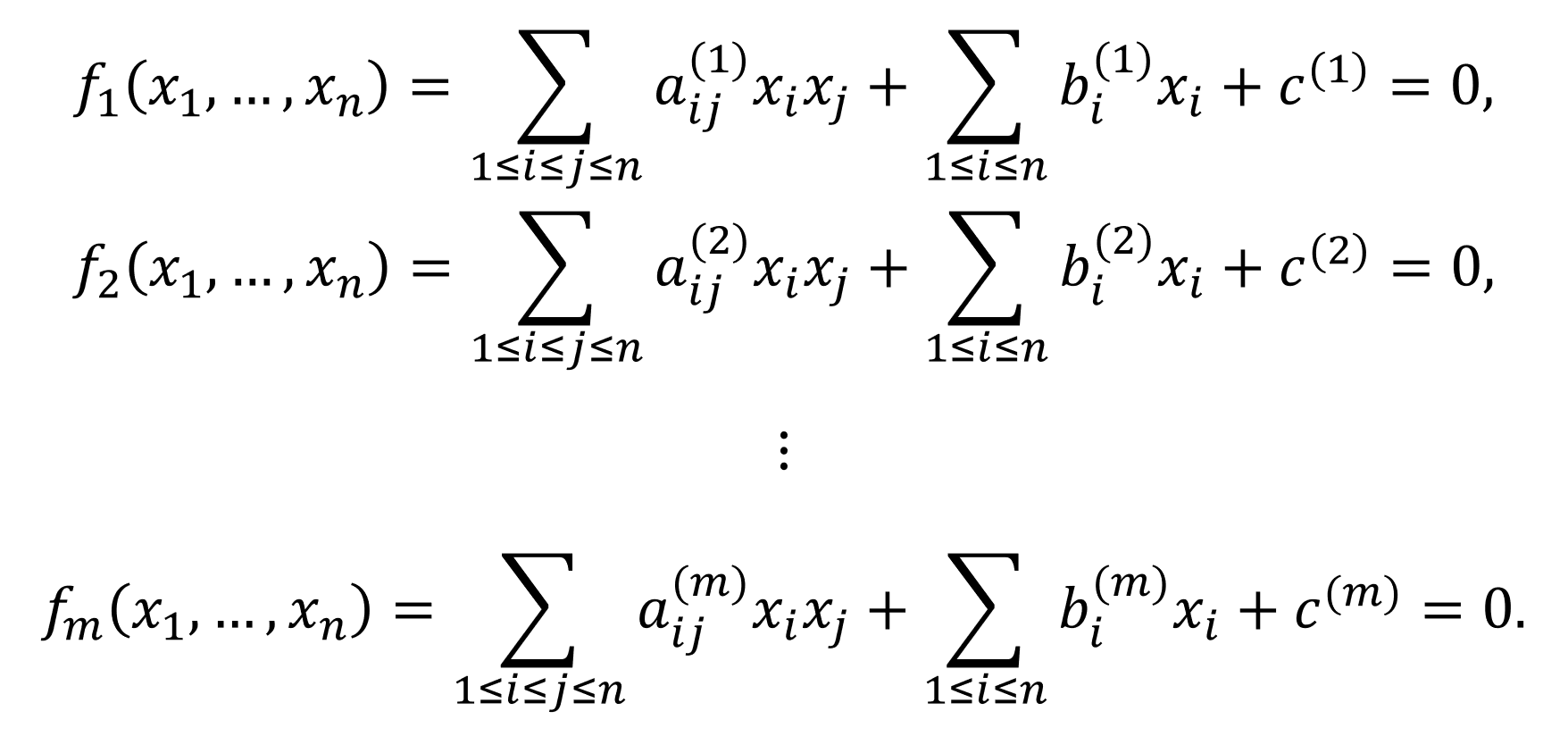
The goal is to find an answer v=[v1,…,vn] in Fn of the above system.
In this challenge, we build up six types of systems: three of them are related to an encryption scheme with three different base fields, and other three are related to a signature scheme.
| Type I: | Encryption, | m=2n, | F=GF(2) |
| Type II: | Encryption, | m=2n, | F=GF(28) |
| Type III: | Encryption, | m=2n, | F=GF(31) |
| Type IV: | Signature, | n≈1.5m, | F=GF(2) |
| Type V: | Signature, | n≈1.5m, | F=GF(28) |
| Type VI: | Signature, | n≈1.5m, | F=GF(31) |
You are welcome to download and solve any challenge and submit the answer to us. We would be glad to see harder problems with larger parameters to be solved. We invite you sincerely to join this challenge and leave your name in the hall of fame.
Reference:
Takanori Yasuda, Xavier Dahan, Yun-Ju Huang, Tsuyoshi Takagi and Kouichi Sakurai,
"MQ Challenge: Hardness Evaluation of Solving Multivariate Quadratic Problems",
presented at the NIST Workshop on Cybersecurity in a Post-Quantum World held in Washington, D.C. on April 2-3, 2015.
Hall of Fame
- Type I
- Type II
- Type III
- Type IV
- Type V
- Type VI
| Number of Variables (n) |
Seed (0,1,2,3,4) | Date | Contestants | Computational Resource |
Data | |
|---|---|---|---|---|---|---|
| 83 | 0 | 2023/09/16 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/almasty/hpXbred, 3488 AMD EPYC 7J13 cores on the Oracle public cloud | Details | |
| 80 | 0 | 2023/07/07 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/almasty/hpXbred, 2048 AMD EPYC 7J13 cores on the Oracle public cloud | Details | |
| 77 | 0 | 2023/06/26 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/almasty/hpXbred, 1024 AMD EPYC 7J13 cores on the Oracle public cloud | Details | |
| 76 | 0 | 2023/06/24 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/almasty/hpXbred, 1024 AMD EPYC 7J13 cores on the Oracle public cloud | Details | |
| 75 | 0 | 2023/06/20 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/almasty/hpXbred, 1024 AMD EPYC 7J13 cores on the Oracle public cloud | Details |
| Number of Variables (n) |
Seed (0,1,2,3,4) | Date | Contestants | Computational Resource |
Data | |
|---|---|---|---|---|---|---|
| 37 | 2 | 2019/04/10 | Takuma Ito, Naoyuki Shinohara, Shigenori Uchiyama | F4-style based algorithm to solve MQ problems, 4 x Intel(R) Xeon(R) CPU E5-4669 v4, 2.20GHz, 1TB RAM | Details | |
| 36 | 0 | 2019/04/10 | Takuma Ito, Naoyuki Shinohara, Shigenori Uchiyama | F4-style based algorithm to solve MQ problems, 4 x Intel(R) Xeon(R) CPU E5-4669 v4, 2.20GHz, 1TB RAM | Details | |
| 35 | 2 | 2016/09/09 | Takuma Ito, Shigenori Uchiyama | modified F4 algorithm, Intel(R) Xeon(R) CPU E5-2620 v4, 2.10GHz, 256GB RAM | Details | |
| Ex. | 20 | 0 | 2015/3/20 | Yun-Ju Huang | Magma F4, Intel(R) Xeon(R) CPU E5-4617, 2.90GHz, 1T RAM | Details |
| Number of Variables (n) |
Seed (0,1,2,3,4) | Date | Contestants | Computational Resource |
Data | |
|---|---|---|---|---|---|---|
| 38 | 3 | 2020/08/03 | Tung Chou, Ruben Niederhagen, Bo-Yin Yang | XL with block Wiedemann, 2x AMD EPYC 7742 | Details | |
| 37 | 1 | 2019/06/27 | Takuma Ito, Naoyuki Shinohara, Shigenori Uchiyama | F4-style based algorithm to solve MQ problems, 4 x Intel(R) Xeon(R) CPU E5-4669 v4, 2.20GHz, 1TB RAM | Details | |
| 37 | 0 | 2020/07/03 | Tung Chou, Ruben Niederhagen, Bo-Yin Yang | XL with block Wiedemann, 2x AMD EPYC 7742 | Details | |
| 36 | 0 | 2016/07/13 | Tung Chou, Ruben Niederhagen, Bo-Yin Yang | XL with block Wiedemann, 4 x AMD Opteron 6282 SE | Details | |
| 35 | 0 | 2015/09/30 | Tung Chou, Ruben Niederhagen, Bo-Yin Yang | XL with block Wiedemann, 4 x AMD Opteron 6282 SE | Details |
| Number of Equations (m) |
Seed (0,1,2,3,4) | Date | Contestants | Computational Resource |
Data | |
|---|---|---|---|---|---|---|
| 76 | 0 | 2024/07/27 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/ almasty/hpXbred, 20480 Intel Xeon Gold 6248 cores on the jean-zay computer @ IDRIS | Details | |
| 75 | 0 | 2024/07/23 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/ almasty/hpXbred, 20480 Intel Xeon Gold 6248 cores on the jean-zay computer @ IDRIS | Details | |
| 72 | 0 | 2024/07/23 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/ almasty/hpXbred, 20480 Intel Xeon Gold 6248 cores on the jean-zay computer @ IDRIS | Details | |
| 71 | 0 | 2024/07/17 | Charles Bouillaguet and Julia Sauvage | https://gitlab.lip6.fr/ almasty/hpXbred, 10240 Intel Xeon Gold 6248 cores on the jean-zay computer @ IDRIS | Details | |
| 69 | 0 | 2020/06/08 | Yao Sun, Ting Li | Improved Parallel Crossbred, Intel i7 8700 (x 8), GeForce GTX 1080Ti (x 10) | Details |
| Number of Equations (m) |
Seed (0,1,2,3,4) | Date | Contestants | Computational Resource |
Data | |
|---|---|---|---|---|---|---|
| 20 | 0 | 2023/08/22 | Ting Li, Yao Sun | 1 x AMD Ryzen Threadripper 3970X, 192GB RAM, 2 x GeForce RTX 3080Ti | Details | |
| 19 | 4 | 2016/05/12 | Wen-Ding Li, Yun-An Chang, Ming-Shing Chen, Chen-Mou Cheng, Bo-Yin Yang | MiniGB-F4, AMD opteron 6376x4 512GB RAM, AMD opteron 6376x4 512GB RAM | Details | |
| 19 | 0 | 2017/10/25 | Rusydi Makarim, Marc Stevens | M4GB, 2 x Intel(R) Xeon(R) CPU E5-2650 v3 @ 2.30GHz, 256GiB RAM | Details | |
| 18 | 0 | 2016/03/11 | Rusydi Makarim, Marc Stevens | M4GB, 2 x Intel(R) Xeon(R) CPU E5-2650 v3 @ 2.30GHz, 256GiB RAM | Details | |
| 18 | 4 | 2016/05/06 | Wen-Ding Li, Yun-An Chang, Ming-Shing Chen, Chen-Mou Cheng, Bo-Yin Yang | MiniGB-F4, Intel(R) Xeon(R) CPU E5620 x 8, Intel(R) Xeon(R) CPU E3-1230 v3, Intel(R) Xeon(R) CPU E3-1245 v3 | Details |
| Number of Equations (m) |
Seed (0,1,2,3,4) | Date | Contestants | Computational Resource |
Data | |
|---|---|---|---|---|---|---|
| 22 | 0 | 2023/11/14 | Kosuke Sakata, Tsuyoshi Takagi | F4 based on Hilbert-driven algorithm, MD EPYC 7742, 2TB RAM | Details | |
| 21 | 0 | 2023/10/23 | Kosuke Sakata, Tsuyoshi Takagi | F4 based on Hilbert-driven algorithm, MD EPYC 7742, 2TB RAM | Details | |
| 20 | 0 | 2017/7/10 | Rusydi Makarim, Marc Stevens | M4GB, 2 x Intel(R) Xeon(R) CPU E5-2650 v3 @ 2.30GHz, 256GiB RAM | Details | |
| 19 | 0 | 2016/3/30 | Rusydi Makarim, Marc Stevens | M4GB, 2 x Intel(R) Xeon(R) CPU E5-2650 v3 @ 2.30GHz, 256GiB RAM | Details | |
| 18 | 0 | 2016/2/29 | Rusydi Makarim, Marc Stevens | M4GB, 1 x Intel(R) Xeon(R) CPU E5-2650 v3 @ 2.30GHz, 128GiB RAM | Details |
The hall of fame lists the five highest positions for each type of systems based on the rules below. For each number of variables n, several seeds are proposed. A participant can choose a seed until he set a record, in which case she will not be able to set a record with the same number of variables n, even with another seed (see Rule 3 below). Here is the full list of all submission details.
Policy and Rules
The policy of this MQ challenge project is to encourage more people all over the world to join the research on solving the MQ problem as well as to motivate the development of the MQ system solvers. Based on this policy, we set up the following rules for the MQ challenge project.
- To encourage the participants, we set up a hall of fame to keep record of participants who could solve a system earlier, as well as for new contributors who could solve harder systems. The one who solved a system with the larger number of variables n will be ranked higher. For participants who solved systems with a same number of variables n (i.e with different seeds) the first one will be ranked higher.
- Concerning challenges with the same number of variables n, only the first five instances solved will be recorded. These five instances should be set up with different seeds.
- To encourage more participants, we allow the submissions of challenges with the same number of variables n (no matter which seed was used) at most once per participant. If one would like to solve more challenges, one should try to solve systems with a larger number of variables n.
- The coefficients of the challenges are generated from the PI digits. For encryption scheme (Type I, Type II, Type III), the MQ challenge team will provide one random answer to make sure the challenges of overdetermined polynomial system have one solution. Hence for, members of MQ challenge team will not participate in solving Type I, Type II and Type III. On the other hand, for signature scheme (Type IV, Type V, Type VI), there are always solutions for underdetermined system. Therefore, the coefficients are all chosen from PI digits, and the MQ challenge team do not know the answers.

